SEEKRANKHEIT
WANN WERDE ICH SEEKRANK ?
Seekrankheit mathematisch berechnet.
Von D.I. Harald Melwisch.

In seinem Buch "Seetüchtigkeit der vergessene Faktor" (1) beschreibt C.A. Marchaj wie ein seetüchtiges Schiff beschaffen sein muss.
Dabei stellt er fest, dass Seetüchtigkeit
nicht nur die mechanische Stabilität und Kentersicherheit betrifft,
sondern auch die Bewegungen die das Schiff in rauer See macht.
Diese Bewegungen sind nämlich dafür
verantwortlich ob die Besatzung seetüchtig bleibt, das beste Schiff
kann verloren
gehen, wenn die Crew im Schwerwetter versagt.
Wo bleibt die Crew länger seetüchtig, in Küstennähe oder weit draussen auf See ?
Auf welchem Schiffstyp bleibt die Crew länger seetüchtig,
auf einem Motorschiff oder Segelschiff ?
Was macht uns seekrank ?
Mediziner erklären uns, dass das Gleichgewichtsorgan der Auslöser des unsicheren Gefühles ist. Allerdings reagiert dieses nicht auf konstante Geschwindigkeit, auch noch nicht auf konstante Beschleunigung, sondern kann offensichtlich Veränderungen der Beschleunigung nicht verkraften.
Die Arbeit des Gleichgewichtsorganes ist dem
Menschen kaum bewusst, dadurch ist es auch schwierig sich vorzustellen
was es stört. Bewegungen unter 3 Sekunden Periode stören es
weniger, vielleicht weil diese für den Körper natürlich
sind weil sie auch bei natürlichen Bewegungen an Land , beispielsweise
beim Laufen, vorkommen.
Ein Schiff kann aber auch sehr grosse Bewegungen
über 3 Sekunden Periode machen.
Der Seegang zwingt einem Schiff eine Bewegung auf welche abhängt von seiner Form, Grösse und Gewicht. Das Schiff überlagert dieser Bewegung seine Eigenschwingungen nach verschiedenen Richtungen als Reaktion auf die Anregung von aussen. Das Ergebnis ist eine komplexe Bewegung von Stampfen, Rollen, Gieren und auf und ab mit einer Vielzahl von Perioden.
Aus einer Grafik in dem Buch Buch "Seetüchtigkeit der vergessene Faktor"(1) kann man die untenstehende Grafik ableiten:
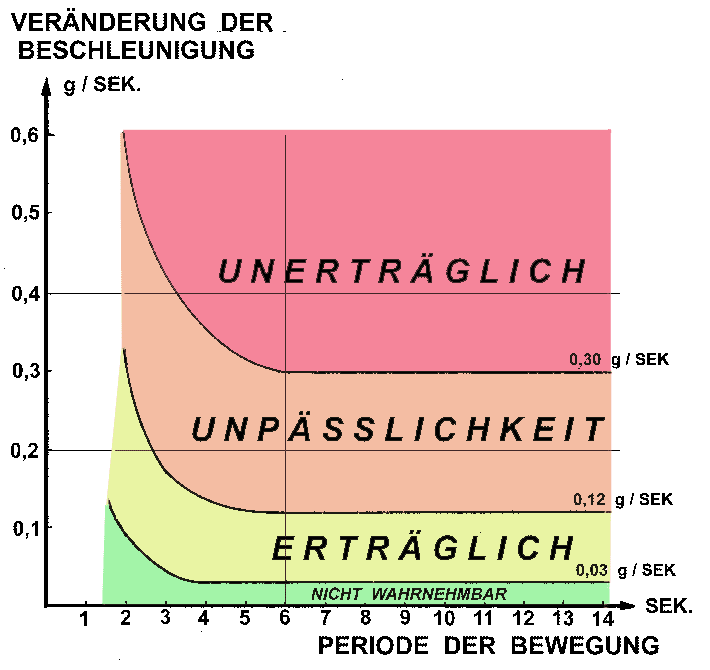
GRAFIK 1: REAKTION DES MENSCHLICHEN KÖRPERS IN
ABHÄNGIGKEIT VON VERÄNDERUNG DER
BESCHLEUNIGUNG UND DER PERIODE .
Die Grafik zeigt, dass der menschliche Körper
auf die Periode der Bewegung reagiert, welcher er ausgesetzt ist, und
auf die Veränderung der Beschleunigung. Auf der Abszisse der Grafik
befindet sich die Periode, auf der Ordinate die Veränderung der Beschleunigung.
Die eingezeichneten Schwellen verlaufen ab Perioden
von 3 Sekunden etwa parallel auf gleicher Höhe, das heisst dass die
Reaktion bei gleicher Veränderung der Beschleunigung gleich ist,
unabhängig von der Periode. Erst bei kleinen Perioden unter 3 Sekunden
wird der Körper widerstandsfähiger, es werden grössere
Werte erträglich.
Die Veränderung der Beschleunigung ist in dieser Grafik der entscheidende Faktor.
Wie gross ist die Veränderung der Beschleunigung ?
Um die Veränderung der Beschleunigung zu
berechnen, ist es einfacher sich eine einzige sinusförmige Bewegung
in einer Richtung vorzustellen.
Wenn die sinusförmige Bewegung eine Halbwellenamplitude
von "So" hat , dann ist die Veränderung der Beschleunigung
:
Ro = So . 25,3 / T 3
Dies ist also der Wert welcher auf der Ordinate
der Grafik bei der jeweils richtigen Periode "T" aufzutragen
ist
(die Berechnung von "Ro" ist im Anhang zu finden) .
"Ro" wird nur linear mit der Amplitude
der Bewegung "So" grösser, sinkt aber mit der dritten Potenz
der Periode "T".
Grosse Perioden können daher in grossen Amplituden auftreten ohne
zu schaden.
1. EIN BEISPIEL :
Ein Schiff fährt in bewegter See langsam gegen Wellen von ca. 3,5 Meter Gesamthöhe und einer Periode von 6 Sekunden. Da die Wellenlänge mit 57 Meter wesentlich grösser ist als die Schiffslänge, macht das Schiff und seine Besatzung die volle Höhenbewegung mit. Die Amplitude der Bewegung ist die Hälfte
der Gesamtbewegung (welche bei Wellen üblicherweise angegeben wird).
So = 1,7 Meter T = 6 Sekunden : Ro
= 1,7 . 25,3 / 216 = 0,2
Trägt man 0,2 auf der Ordinate bei T=6 auf, kommt man Mitten ins Gebiet der Unpässlichkeit zu liegen.
Seekrankheit ist die Folge.
Die Bewegungen eines Schiffes setzen sich, wie schon weiter oben gesagt, zusammen aus den Bewegungen welche der Seegang dem Schiff aufzwingt, plus den Schwingungen der Eigenfrequenzen des Schiffes für Stampfen und Rollen, welche das Schiff addiert.
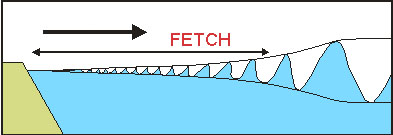
2. EIN SCHIFF IN KÜSTENNÄHE UND WEITER DRAUSSEN :
| Ein Wind mit Beaufort 6 verursacht nach einer Anlaufstrecke (fetch) von 10 Seemeilen, also beispielsweise 10 Seemeilen von Land, Wellen von 0,86 Meter Höhe, 28 Meter Länge und einer Periode von 4,2 Sekunden. Wenn wir annehmen in einem kleinen Schiff
zu sitzen welches diese Bewegungen mitmacht, dann können wir
mit So = 0,43 |
|
Ro = 0,146
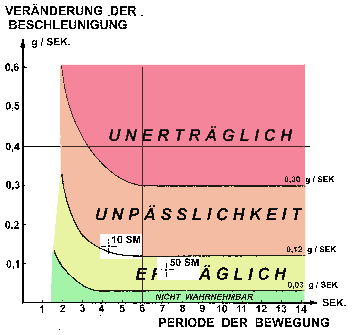
In der Grafik (siehe unten) kommt dieser Punkt schon im Bereich der Unpässlichkeit zu liegen.
Derselbe Wind von Bft. 6 verursacht auf See nach einer Anlaufstrecke von 50 Seemeilen Wellen von 2,53 Meter Höhe, 83 Meter Länge und einer Periode von 7,2 Sekunden. "So" wird die Hälfte von 2,53 und T = 7,2. "Ro" errechnet sich zu: Ro = 0,086 Aufgrund der wesentlich grösseren Wellenhöhe,
nämlich 2,53m statt 0,86 m, wäre hier eher Seekrankheit
zu erwarten. Wir liegen 50 Seemeilen vom Land entfernt trotz höherer Wellen also günstiger. Generell gilt, dass höhere Wellen
grössere Perioden haben. Dadurch werden sie angenehmer, da
"Ro" kleiner wird. |
GRAFIK 2: DIE PUNKTE FÜR WINDSTÄRKE
6 IN GEBIETEN MIT ANLAUFSTRECKEN |
Für geringe Wellenhöhen gilt noch folgende Überlegung :
Im offenen Seegebiet haben Wellen von 0,3 - 0,5
Meter Höhe Perioden von 2 - 3 Sekunden. Die Länge dieser
Wellen ist
allerdings in der Grösse der Länge von Sportbooten. Dadurch
macht das Schiff die Bewegung der Welle nicht mehr voll mit
und mildert die Wirkung.
Ab 1 Meter Wellenhöhe und 4 Sekunden Periode wird die Länge allerdings doppelt so lang, das Schiff macht die Bewegung wieder mit. Ab hier beginnt eine kritische Periodengrösse für Sportboote.
Für grosse Wellenhöhen muss noch bedacht werden :
Grosse Wellen in der Windsee sind weit weg von
sinusförmig. Sie bilden spitze Wellenkämme durch die Orbitalbewegung
der Wasserteilchen. Bei weiterer Erhöhung brechen sie und bilden
zusätzliche Wellenbewegungen innerhalb der Wellenperioden.
Beides bedeutet Bewegungen von kürzeren Perioden innerhalb der Welle
mit grosser Periode. Diese kürzeren Perioden machen seekrank, um
so mehr als diese zusätzlichen Bewegungen nicht periodisch sondern
unvermutet erfolgen.
Wellen mit Grundperioden von mehr als 10 Sekunden
wären, auch wenn sie 10 Meter hoch sind, in reiner Sinusform nicht
würdig seekrank zu werden.
Die schnelleren Zusatzformationen einer Windsee sind es welche dem menschlichen
Körper Probleme bereiten.
3. EIN SCHIFF DESSEN EIGENFREQUENZEN ANGEREGT WERDEN :
Ein Schiff hat, wie jeder mechanische Körper, in verschiedene Bewegungsrichtungen verschiedene Trägheitsmomente und damit Eigenfrequenzen. Am ausgeprägtesten sind bei Schiffen Rollen und Stampfen. Beide können, wenn sie durch einen Seegang ähnlicher Periode angeregt werden, recht unangenehm werden.
Wir wollen als Beispiel hier Stampfen betrachten.
Wellen sind an ihrer Oberfläche nicht sinusförmig. Die rotierende Bewegung der Teilchen unter Wasser sorgt zusammen mit der Fortpflanzungsgeschwindigkeit dafür dass spitze Wellenkämme entstehen. Der Wind fördert das zusätzlich, weil er am aufsteigenden Wellenkamm Widerstand findet .
Wenn ein Schiff über diese Wellenkämme
fährt, dann fällt es beim passieren jedes Wellenkammes nach
vorne und macht eine
Stampfbewegung die mit seiner Eigenfrequenz für Stampfen ausschwingt.
Wir wollen ein Segelboot und ein Motorboot betrachten beim stampfen gegen die Wellen:
Ein Segelboot muss dabei sowohl sein hohes Rigg, als auch den manchmal beschwerten Kiel mitdrehen. Dadurch wird die Periode des Ausschwinges (1):
T = K . Wurzel (Länge) K = 1,3 ... 1,6 ( Beispiel: 1,45 )
Ein 13 Meter langes Segelschiff erzeugt dabei eine Periode des Stampfens von:
T = 1,45 . Wurzel (13 ) = 5,23 Sekunden Wenn wir beispielsweise annehmen dass eine Person achtern in der Plicht sitzt, 0,3 fache Schiffslänge vom Drehpunkt des Schiffes entfernt, und die Ausschwingbewegung im Mittel plus- minus 4 Grad Stampfwinkel verursacht, dann macht diese Person ein "So" von 0,272 Meter. "Ro" errechnet sich mit T = 5,23 zu: Ro = 0,048 |
 |
Dieser Wert eingetragen in die Grafik gibt
Entwarnung: Der Punkt liegt im unteren Bereich des Erträglichkeitsbereiches
und
wird kaum zusätzlich zu den wellenbedingten Bewegungen Seekrankheit
verursachen.
Ein Motorboot hat eine kleinere Eigenfrequenz für
Stampfen. T = K . Wurzel (Länge) K = 0,4 ... 0,9 ( Beispiel: 0,7 ) Ein wieder 13 Meter langes Motorboot erzeugt also beim Ausschwingen eine Periode von T = 0,7 . Wurzel (13 ) = 2,52 Sekunden Wenn wir wieder annehmen dass eine Person 0,3 fache Schiffslänge vom Drehpunkt entfernt sitzt und die Ausschwingbewegung im Mittel plus- minus 4 Grad Stampfwinkel verursacht, dann macht diese Person wieder ein "So" von 0,272 Meter. "Ro" errechnet sich mit T = 2,52 zu: Ro = 0,43 |
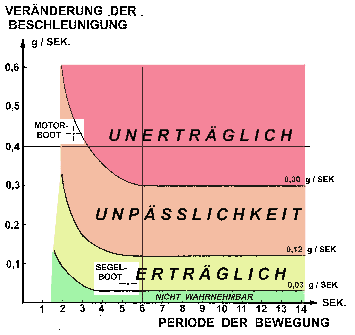
GRAFIK 3: DIE PUNKTE FÜR EIN SEGELBOOT UND EIN MOTORBOOT MIT 4 GRAD STAMPFAMPLITUDE MIT SEINER EIGENFREQUENZ . |
Dieser Wert eingetragen in die Grafik bei T = 2,52 gibt Grund zur Besorgnis: Der Punkt liegt knapp am Bereich der Unerträglichkeit, und er repräsentiert nur die Eigenschwingungen, ohne die Bewegungen durch die Wellen selbst. Wehe wenn dieses Boot in eine Welle bekommt welche zusammen mit seiner Fahrgeschwindigkeit eine Periode um 2 - 3 Sekunden erzeugt und seine Eigenschwingung noch anregt und verstärkt ! |
 |
Ist das einer der Gründe warum ein Segelboot im Seegang als seetüchtiger angesehen wird als ein gleichgrosses Motorboot ?
D.I. Harald Melwisch
Lit (1): C.A. Marchaj "Seetüchtigkeit der vergessene Faktor"
, Delius Klasing Verlag
ANHANG : Die Berechnung der Veränderung der Beschleunigung :
Um die Veränderung der Beschleunigung zu
berechnen, ist es einfacher sich eine einzige sinusförmige Bewegung
in einer Richtung vorzustellen:
S = So . sin ( 2.pi.t / T )
S........ momentaner Weg des Körpers (Meter)
So...... Amplitude des Weges der Bewegung. Hier gilt der Spitzenwert,
also vom Mittelpunkt in eine Richtung.
z.B: Eine Person welche im stampfenden Schiff eine Gesamtbewegung von
0,4 Meter macht, hat ein "So" von 0,2 Meter
vom Mittelpunkt auf und ab.
t...........Zeit (Sekunden)
T..........Periode der Bewegung, also die Zeitdauer einer Auf- und Abbewegung (Sekunden).
Die Geschwindigkeit des Körpers ergibt sich durch einfaches differenzieren von "S" nach der Zeit:
V = So . ( 2.pi / T ) . cos ( 2.pi .t / T )
V..........momentane Geschwindigkeit (Meter pro Sekunde)
Die Beschleunigung und letztlich die Veränderung der Beschleunigung des Körpers ergibt sich durch jeweils nochmaliges differenzieren nach der Zeit. Jedesmal entsteht ein Faktor "2.pi / T" vor der Winkelfunktion:
R = - So . ( 2.pi / T )3 . cos ( 2.pi.t / T ) = - Ro . cos ( 2.pi.t / T )
R...........momentane Veränderung der Beschleunigung (Meter pro Sekunde2 pro Sekunde)
Ro.........Amplitude der Veränderung der Beschleunigung (Meter pro Sekunde2 pro Sekunde).
Von diesem Wert interessiert uns nur die Amplitude "Ro", also der Wert vor der Winkelfunktion.
Ro = So . ( 2.pi / T )3
"Ro" ist die Veränderung der Beschleunigung
in der Einheit "Meter pro Sekunde2 pro Sekunde".
In die Grafik ist die Beschleunigung als Vielfache
der Erdbeschleunigung "g" einzutragen . Die Erdbeschleunigung
ist 9,81 Meter pro Sekunde2 .
Dividiert man also "Ro" durch 9,81 um vielfache der Erdbeschleunigung zu bekommen und setzt gleichzeitig für ( 2.pi ) 3 den Zahlenwert 248 ein,dann bekommt man für "Ro" :
Ro = So . 25,3 / T 3
Dies ist also der Wert welcher auf der Ordinate der Grafik bei der jeweils richtigen Periode "T" aufzutragen ist.
"Ro" wird nur linear mit der Amplitude
der Bewegung "So" grösser, sinkt aber mit der dritten Potenz
der Periode "T".
Grosse Perioden können daher in grossen Amplituden auftreten ohne
zu schaden.